Orbital Fractal Overview
The Fractal Science Kit fractal generator Orbital fractals collect statistics during the orbit of a fractal formula and use these to create the fractal image. In contrast to Mandelbrot Fractals where we generate an orbit for each pixel in the viewing window to produce a picture, Orbital fractals generate a single orbit and we keep track of all the points we visit during the orbit along with how many times we visit each point, what part of the fractal formula caused us to visit the point (the attractor index), the speed/acceleration of the orbit at that point, etc. These data values are used to color the fractal. This process is sometimes called the Chaos Game (Wikipedia).
Sierpinski Triangle
The classic example of an Orbital fractal is the Sierpinski Triangle (Wikipedia).
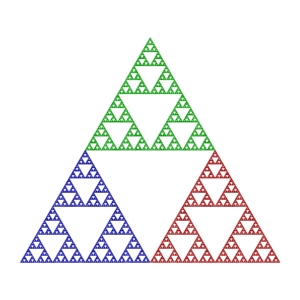
A Fractal Science Kit fractal program to generate a Sierpinski Triangle fractal follows:
global:
const Complex v[] = 1i, -0.866-0.5i, 0.866-0.5i
iterate:
attractorIndex = Random.Integer(3)
z = (z + v[attractorIndex])/2
The array v[] contains the vertices of an equilateral triangle on the complex plane. On each iteration, we select a vertex of the equilateral triangle at random and move the orbit point to the midpoint of the segment that connects the current point to the selected vertex. The Sierpinski Triangle is the result!
Sierpinski N-gons, IFS fractals, Strange Attractors, Dragon Flames, Rep-N Tiles, Apollonian Gasket fractals, Circle Inversion fractals, Kleinian Group fractals, Symmetric Icons, Symmetric Attractors, Mobius Dragon IFS, Mobius Patterns, Grand Julian IFS, Elliptic Splits IFS, Splits Ngon fractals, Frieze Group Attractors, Wallpaper Group Attractors, and Hyperbolic Attractors, are all examples of Orbital fractals.
Sierpinski N-gons
Sierpinski N-gons are a generalization of the
Sierpinski Triangle
(Wikipedia) attractor based on a polygon with N
vertices. A Sierpinski N-gon is defined as a set of
transformations about the vertices of a regular polygon. During the fractal
iteration, one of the vertices is selected at random, and the current orbit
point is passed through the associated transformations to obtain the next orbit
point. Variations of this algorithm include points in addition to the polygon
vertices and allow control of the individual transformations about each point.
IFS Fractals
IFS
(Iterated Function System) fractals are defined as a set of affine
transformations (usually), each assigned a probability value. During the fractal
iteration, one of the transformations is selected at random based on the
assigned probabilities, and the current orbit point is passed through the
selected transformation to obtain the next orbit point. In general, in order to
produce a fractal, the transformations should be contractions; i.e., when
applied to any 2 points, the transformation should reduce the Euclidean distance
between the points. Programs to display example IFS fractals and to
search for different combinations of parameters that produce interesting results
are provided. See
Iterated
function system (Wikipedia) for additional details.
Strange Attractors
Strange Attractors are defined by an equation or
system of equations. The orbit points are generated by passing the current orbit
point through the equations to obtain the next orbit point. This process is
repeated thousands (or millions) of times to produce the fractal data. Of
course, most equations will not produce a fractal and the challenge is to find
equations that do. Quadratic Attractors and
Cubic Attractors are examples of these fractal types. Programs to
display examples of these fractals and to search for different combinations of
parameters that produce interesting results are provided. See
Attractor (Wikipedia) for
additional details.
Rep-N Tiles
Rep-N Tiles (replicating figures on the plane)
are attractors based on a set of N affine transformations that generate a
Rep-N Tile. Omitting 1 or more of the
transformations and passing the orbit points through a symmetry transformation
results in highly complex, and beautiful, symmetric designs. The term
Rep-Tile was coined by Solomon W. Golomb in 1962.
See Rep-Tile (MathWorld)
for additional details.
Apollonian Gasket Fractals
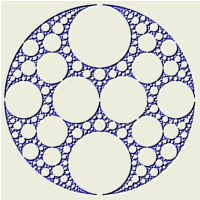Apollonian Gasket fractals are fractals based on
2 pairs of Mobius transformations. The Apollonian Gasket, and the methods used
to produce them, are described in the excellent book
Indra's
Pearls - The Vision of Felix Klein by David Mumford, Caroline Series,
and David Wright. These fractals are usually displayed using a deterministic
algorithm (see the Apollonian Gasket
Orbit Trap) which
produces the best results; however, the Orbital fractal images are still quite impressive.
For additional details, see David Wright's Indra's
Pearls site and
Apollonian Gasket (Wikipedia).
Circle Inversion Fractals
Circle Inversion fractals are defined by a set
of mutually tangent circles. During the fractal iteration, one of the circles is
selected at random, and the current orbit point is reflected in the circle to
obtain the next orbit point. As usual, this process is repeated thousands of
times to produce the fractal data. The process of reflecting a point in a circle
is called inversion. See
Circle
Inversion Fractals (Yale) for additional details.
Kleinian Group Fractals
Kleinian Group
fractals are fractals based on 2 pairs of Mobius transformations and allow you
to produce Quasifuchsian, Single Cusp, and Double Cusp, Two-Generator Group
fractals described in the book
Indra's
Pearls - The Vision of Felix Klein by David Mumford, Caroline
Series, and David Wright. These fractals are usually displayed using a deterministic
algorithm (see the Kleinian Group
Orbit Trap) which
produces the best results; however, the Orbital fractal images are still quite impressive.
For additional details, see David Wright's Indra's
Pearls site.
Symmetric Icons
Symmetric Icons are strange attractors that
produce symmetric designs based on the equations given in the book
Symmetry in Chaos by Michael Field and Martin
Golubitsky. Programs to display example Symmetric Icons
along with programs to search for interesting sets of parameters are included.
See Images of Chaos and
Symmetry for
additional details.
Symmetric Attractors
Symmetric Attractors are strange attractors that
produce symmetric designs based on equations given in the paper
Chaotic attractors with cyclic
symmetry revisited, by Kevin C. Jones and Clifford A. Reiter (Lafayette
College). See
References for details. Programs to display example
Symmetric Attractors,
along with programs to search for interesting sets of parameters are included.
See Clifford A. Reiter's
Gallery
of Fractals, Chaos and Symmetry for additional details.
Mobius Dragon IFS Fractals
Mobius Dragon IFS fractals are generated by an IFS formed from a set of Mobius Transformations using the Orbital Equation Mobius Dragon IFS. The Mobius Dragon IFS equation is based on information given by penny5775 on the pages Mobius-Dragon-Script and Mobius-Design-Pack. Note that the information found on these pages relates to the Apophysis fractal generator not the Fractal Science Kit but is included here for reference.
Mobius Patterns
Mobius Patterns are
generated by an
IFS formed from a set of Mobius
Transformations using the
Orbital Equation
Mobius Patterns. The Mobius Patterns
equation is based on information found
in the excellent book
Indra's
Pearls - The Vision of Felix Klein by David Mumford, Caroline Series, and David Wright.
For additional details, see David Wright's Indra's
Pearls site.
Grand Julian IFS Fractals
Grand Julian IFS
fractals are generated by an IFS using the the
Orbital Equation
Grand Julian IFS.
Elliptic Splits Fractals
Elliptic Splits IFS fractals are based on the Orbital Equation Elliptic Splits IFS. The Elliptic Splits IFS equation is based on information given by SaTaNiA on the page Tutorial - Splits elliptic. Note that the information found on this page relates to the Apophysis fractal generator not the Fractal Science Kit but is included here for reference.
Splits Ngon Fractals
Splits Ngon fractals are based on the
Orbital Equation Flame
(4 Transforms). The Splits Ngon fractals are based on information given by
guagapunyaimel on the page
Splits-Ngon
Tutorial. Note that the information found on this page relates to the
Apophysis fractal generator not the Fractal Science Kit but is included here for
reference.
Frieze Group and Wallpaper Group Attractors
Frieze Group and
Wallpaper Group attractors are strange attractors that
produce symmetric designs based on the 7 one-dimensional frieze group patterns
and the 17 two-dimensional wallpaper group patterns. A discussion of algorithms
to produce these attractors is given in the paper
Chaotic
Attractors with Discrete Planar Symmetries, by Nathan C. Carter,
Richard L. Eagles, Stephen M. Grimes, Andrew C. Hahn, and Clifford A. Reiter
(Lafayette College). Programs to display example Frieze Group patterns
and
Wallpaper Group patterns, along with programs to search for interesting sets of parameters are included.
See Clifford A. Reiter's
Gallery
of Fractals, Chaos and Symmetry for additional details.
These patterns can also be formed from any attractor using the Symmetry Transformations Plane Symmetry Groups - Square Lattice or Plane Symmetry Groups - Hexagonal Lattice.
Hyperbolic Attractors
Hyperbolic
Attractors are strange attractors that
produce designs with hyperbolic symmetry. A discussion of algorithms to produce
these attractors is given in the paper
Iterated function systems with
symmetry in the hyperbolic plane, by Bruce M. Adcock, Kevin C. Jones, Clifford A. Reiter
(Lafayette College), and Lisa M. Vislocky. See
References for details. See Clifford A. Reiter's
Gallery
of Fractals, Chaos and Symmetry for additional details.
These patterns can also be formed from any attractor using the Symmetry Transformation Plane Hyperbolic Tiling - Orbital.
Hyperbolic Mobius Fractals
Hyperbolic Mobius
fractals are generated by an IFS formed from a set of Mobius
Transformations using the
Orbital Equation
Mobius Patterns and then passing the results through the
Symmetry Transformation
Plane Hyperbolic Tiling - Orbital. The Mobius Patterns
equation is based on information found
in the excellent book
Indra's
Pearls - The Vision of Felix Klein by David Mumford, Caroline Series, and David Wright.
For additional details, see David Wright's Indra's
Pearls site.
Built-in Orbital Equations
The
Fractal Science Kit fractal generator has over 50 built-in Orbital Equations including Sierpinski Triangle,
Sierpinski N-gons, Koch
Snowflake, Apollonian
Gasket, Circle Inversion fractals,
Kleinian Group fractals,
Dragons, Dimers, Rep-N Tiles, IFS
fractals, Quadratic Attractors,
Cubic Attractors,
Symmetric Icons, Symmetric
Attractors, Mobius Dragon IFS,
Mobius Patterns, Grand Julian
IFS, Elliptic Splits IFS,
Frieze Group,
Wallpaper Group,
Hyperbolic Attractors, and many more. Many of these
programs define properties that can be used to produce countless different
variations. Some of the programs search for interesting parameter settings based
on user defined criteria and produce unique fractals every time they are run!
See Built-in Orbital Equations
for a complete list.